Language models and text generation using LSTMs
The code included here is available on my GitHub repo.
Introduction to language models
Natural language processing (NLP) is a sub-field of artificial intelligence. In short, NLP processes the human language; it learns the behaviour and patterns within the human language in order to process, understand, and even generate text. Considering the complexity of linguistics, it is not hard to see why this would be a very difficult task for a computer. The spoken and written language not only depends on the order but the context of individual words and characters that make up the corpus. Consider the following excerpt:
The Sun shines brighter than any other star in our solar system. I have seen it with my very own eyes at the edge of our universe. I couldn't help but turn my head away to not stare directly into its brilliance. It continued to burn throughout the day.
Here, what is the author referring to in their last sentence when they say it? To us, it is obvious that they are talking about the Sun. However, to a computer this might not be very obvious. The computer lacks context - it needs to be trained on similar text data in order to make inferences and deduce what it is.
Text generation falls under the umbrella of NLP; it involves a model providing a text output based on a text input. The general idea here is to train a model using a large set of text data, provide a text prompt, and receive an output which is concatenated to the prompt - this process will loop.

Tokens, indices, and the probability mass function
Several terms are defined as follows:
A corpus is large, unstructured text.
A token is the basic unit of a language model; it is a string of contiguous characters. A token can be a word, a character, a symbol, or a number. The process of converting the corpus to individual tokens is called tokenization.
Tokens can be at the level of words, characters, or n-grams. N-grams are a continuous sequence of characters of the specified length, n.
A vocabulary is the number of unique tokens. (I.e., returned by Python's set command across a tuple of text input).
An index represents each token in a dictionary.
A probability mass function is analogous to a probability density function, except it is concerned with discrete random variables and not continuous variables. It describes a function that yields a probability that a discrete random variable equals some value, such that:
\(p_{X}(x) = P(X = x)\) for \(-\infty < x < \infty\)
- Then, the conditional probability of discrete variable A given another discrete variable B is defined as:
\(P(A|B) = \frac{P(A \cap B)}{P(B)}\)
In brief, text input data is tokenized first and then converted to a sequence of indices. In Python using Tensorflow and Keras, this is typically done using fit_on_text - which creates the vocabulary index - and texts_to_sequences - which transforms the text to a sequence of integers. An example code for this process was described in my previous post on NLP. Briefly, assuming a vector X of length n which contains the text data used to train a model:
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
max_words = 2000
max_len = 100
tokenizer = Tokenizer(num_words=max_words)
tokenizer.fit_on_texts(X)
X = tokenizer.texts_to_sequences(X)
X = pad_sequences(X, padding='post', maxlen=max_len)Note we've ensured that our sequences are all of the same length using the pad_sequences function, which will concatenate a string of zeros to our contiguous sequences.
N-grams and the Markov assumption
N-grams are generalized tokens of length n and are analogous to the concept of k-mers in computational biology. In a language model with some hyperparameter n, the Markov assumption can be made to simplify the probability distribution of each token in a vocabulary. The Markov assumption states that the future state depends only on the previous state. Therefore, in a bi-gram model (n = 2):
\(p(w) = \prod_{i = 1}^{k + 1} p(w_{i}|w_{i - 1})\)
In other words, the probability of each word in a given sequence depends on its previous state. Generalizing to any n, this means that the next event in a sequence depends only on its immediate past. Using this assumption as the conditional probability mass function, the text generation model can output a word or a character based on the input seed sequence.
Recurrent neural networks (RNN)
In contrast to the assumption of the Markov chain, recurrent neural networks (RNNs) deploy a memory state. The defining characteristic of an RNN versus a simple stacked dense layer network is the concept of memory; it iterates through the data and maintains an internal loop, maintaining a state containing information relative to the past information. This characteristic allows RNNs to be suitable for handling sequence data. A bidirectional long short term memory (LSTM) RNN was used in my previous post on NLP classification.
Training an RNN involves a process called back propagation through time (BPTT). In a typical feed-forward network, back propagation uses a measurement of error (i.e., loss metric) to calculate the gradient at each layer, which indicates the extent to which the weights of each layer is adjusted. The process of gradient descent is described in one of my previous posts. In an RNN, this back propagation process occurs through the length of our input sequence, as such:
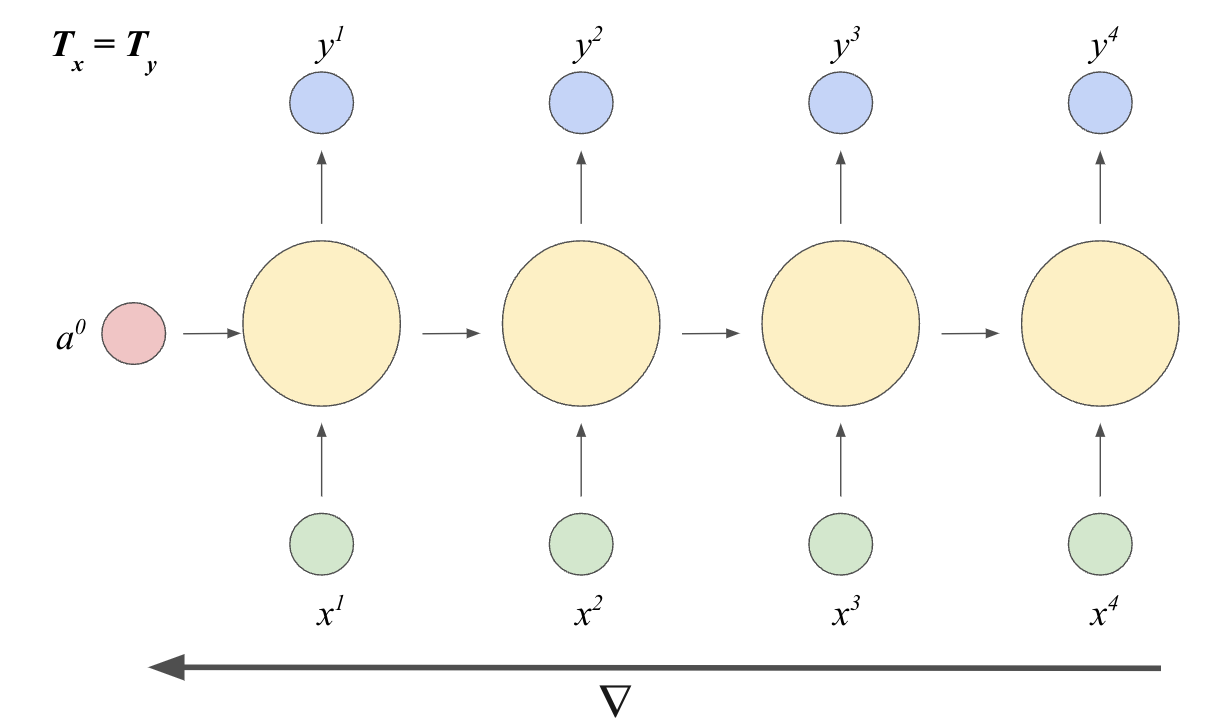
Above is an example RNN in a many-to-many prediction task, such that the input and the output sequence length is both greater than one. The input sequence is tokenized into length k (in above case, k = 4) and each token is input sequentially with the hidden state a to output y. The initial hidden state \(a_{0}\) is random while the subsequent hidden states \(a_{k}\) carries past information through time learned from the previous layer by applying a linear transformation over the previous step and the current input \(x_{k}\). In other words, for the kth layer:
\(a_{k} = f_{1}(W_{aa}a_{k-1} + W_{ax}x_{k} + b_{a})\)
The output y is then a transformation of the hidden state \(a_{k}\) and the weight:
\(y_{k} = g_{2}(W_{ya}a_{k} + b_{y})\)
Common activation functions (i.e., \(g_{1}\), \(g_{2}\)) used in RNNs include tanh, sigmoid, and relu functions.
The BPTT algorithm attempts to adjust the weights by minimizing some loss function. Instead of propagating through the densely stacked layers as in typical deep neural networks, the gradient is calculated through the sequence layers in an RNN. This means that the gradient \(\nabla\) passes through usually very deep networks. This can cause a typical problem in RNNs called the vanishing gradient problem, which minimizes the contribution of earlier sequence tokens (i.e., as the gradient becomes smaller and smaller the further we propagate backwards in time). In other words, the model has short-term memory.
An algorithm such as an LSTM which carries information across many time steps allow it to be generalizable rather than learn specific patterns. This is pertinent in the case of text generation and tackles the problem of the vanishing gradient problem. LSTM achieves this by storing long term memory called the cell state on top of the working memory that is the hidden state. This increases the complexity of the model (which comes with its own problems, such as the variance and bias trade-off) but significantly enhances the ability to deal with long-term dependencies.
Text generation using LSTMs
Text generation with LSTMs can be implemented in Python using TensorFlow and Keras. Here, I am using Google Colab to execute the following code.
import numpy as np
import pandas as pd
import tensorflow as tf
from tf.keras.models import Sequential
from tf.keras.layers import Dense
from tf.keras.layers import LSTM
from tf.keras.optimizers import RMSprop
from tf.keras.utils import to_categorical
from tf.keras.preprocessing.sequence import pad_sequencesHere, I am using Jane Austen's Persuasion as training data for the text generation model. This book (and many other books) can be downloaded for free in plain text version here. I downloaded Persuasion and uploaded it to my Colab working directory.
After loading the book, I created two dictionaries which map individual characters to numerical indices and vice versa. This is required as character input is not suitable for the neural network. As I've mentioned before, this can be done using Keras' tokenizer functions or done manually as below.
filename = 'persuasion_jane_austen.txt'
raw_text = open(filename, 'r', encoding='utf-8').read()
raw_text = raw_text.lower()
chars = sorted(list(set(raw_text)))
char_indices = dict((c, i) for i, c in enumerate(chars))
indices_char = dict((i, c) for i, c in enumerate(chars))The target and the predictors (X and y) are n-grams and the following character. For example: X = 'FLOWE' and y = 'R'. To implement this, I define maximum sequence length (max_len) and read across the entirety of the corpus. Then the sequences are converted to numerical values using the char_indices dictionary.
max_len = 100
dx = []
dy = []
for i in range(0, len(raw_text) - max_len, 1):
dx.append(raw_text[i : i + max_len])
dy.append(raw_text[i + max_len])
X = []
for i in range(0, len(dx), 1):
X.append([char_indices[a] for a in dx[i]])
y = []
for i in range(0, len(dy), 1):
y.append([char_indices[a] for a in dy[i]])
y = [a[0] for a in y] Due to the size of the training data, running the model on the entire corpus is computationally expensive. For example, fitting an LSTM model on the data over 10 epochs took over 5 hours of run time on Colab. Therefore, for the sake of this exercise I am limiting myself to the first 50000 sequences.
Prior to model training, the target variable must be one-hot encoded. This is done using Keras' to_categorical.
X2 = X[0:50000]
X2 = np.reshape(X2, (len(X2), max_len, 1))
X2 = X2 / float(len(chars))
y2 = to_categorical(y)
y2 = y2[0:50000]Here I am compiling a relatively small LSTM model with a single dropout layer. I adjusted the learning rate on the RMSprop optimizer and set clipnorm to avoid exploding gradient.
model = Sequential()
model.add(LSTM(128, input_shape=(X2.shape[1], X2.shape[2])))
model.add(Dropout(0.2))
model.add(Dense(y2.shape[1], activation='softmax'))
optimizer = RMSprop(learning_rate=0.01, clipnorm=1)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)
model.summary()
I'm fitting the model over 30 epochs and it took around 45 minutes of run-time.
model.fit(X2, y2, epochs=30, batch_size=128, verbose=0)Finally, I am taking an example text from another one of Jane Austen's books (Pride and Prejudice) in order to test whether the model can generate text in an iterative manner.
new = 'He had always intended to visit him, though to the last always assuring his wife that he should not go; and till the evening after the visit was paid she had no knowledge of it. it was then disclosed in the following manner. observing his second daughter employed in trimming a hat, he suddenly addressed her with'
new = new.lower()To construct the iterative text generation process, I wrote a for-loop that iterates over user-defined range. This is done by predicting the next character using the seed sequence (i.e., user input) and then concatenating the seed to the predicted character, then using that new sequence as the new seed.
def generate_chars(seed, length, model, maxlen):
sentence = seed
for i in range(length):
seed_list = []
for a in range(0, len(sentence), 1):
seed_list.append([char_indices[j] for j in sentence[a]])
seed_list_padded = pad_sequences([seed_list],
maxlen = maxlen, padding='pre')
seed_list_padded = seed_list_padded / float(len(chars))
pred = model.predict(seed_list_padded, verbose=0)[0]
pred = np.argmax(pred)
pred = indices_char[pred]
sentence += pred
return(sentence)Running the function on the defined seed sequence generates some characters that are mostly nonsensical, but there are a few coherent words including the, of, her, father, and and. Of course, in terms of context the generated text makes no sense. However, I've used a small, simple model with minimal regularization and a fraction of the initial corpus as the training data. Hardware limitations and run-time issues aside, the LSTM model has successfully executed the iterative text generation process.
generate_chars(seed=new, length=50, model=model, maxlen=max_len)'he had always intended to visit him, though to the last always assuring his wife that he should not go; and till the evening after the visit was paid she had no knowledge of it. it was then disclosed in the following manner. observing his second daughter employed in trimming a hat, he suddenly addressed her with ann the ceninnen of her father saseinen and annen'Summary
Human linguistics are complex and next-generation models have continued to decipher the character-to-character relationships. Language models deploy memory states in order to store long- and short-term memory in order to carry information forward. Text generation is a component of language models and is an iterative process where the predicted character/word is concatenated to the input in order to predict the next character/word. As one can imagine, this algorithm is ubiquitous in today's technology and even relatively simple models have the ability to generate text.